Yi-Cheng liu

Yi-Cheng liu

1st year ECE MS student at UMich. Specialized in Robotics, Controls system

Error-State Extended Kalman Filter for Vehicle Localization

Goal

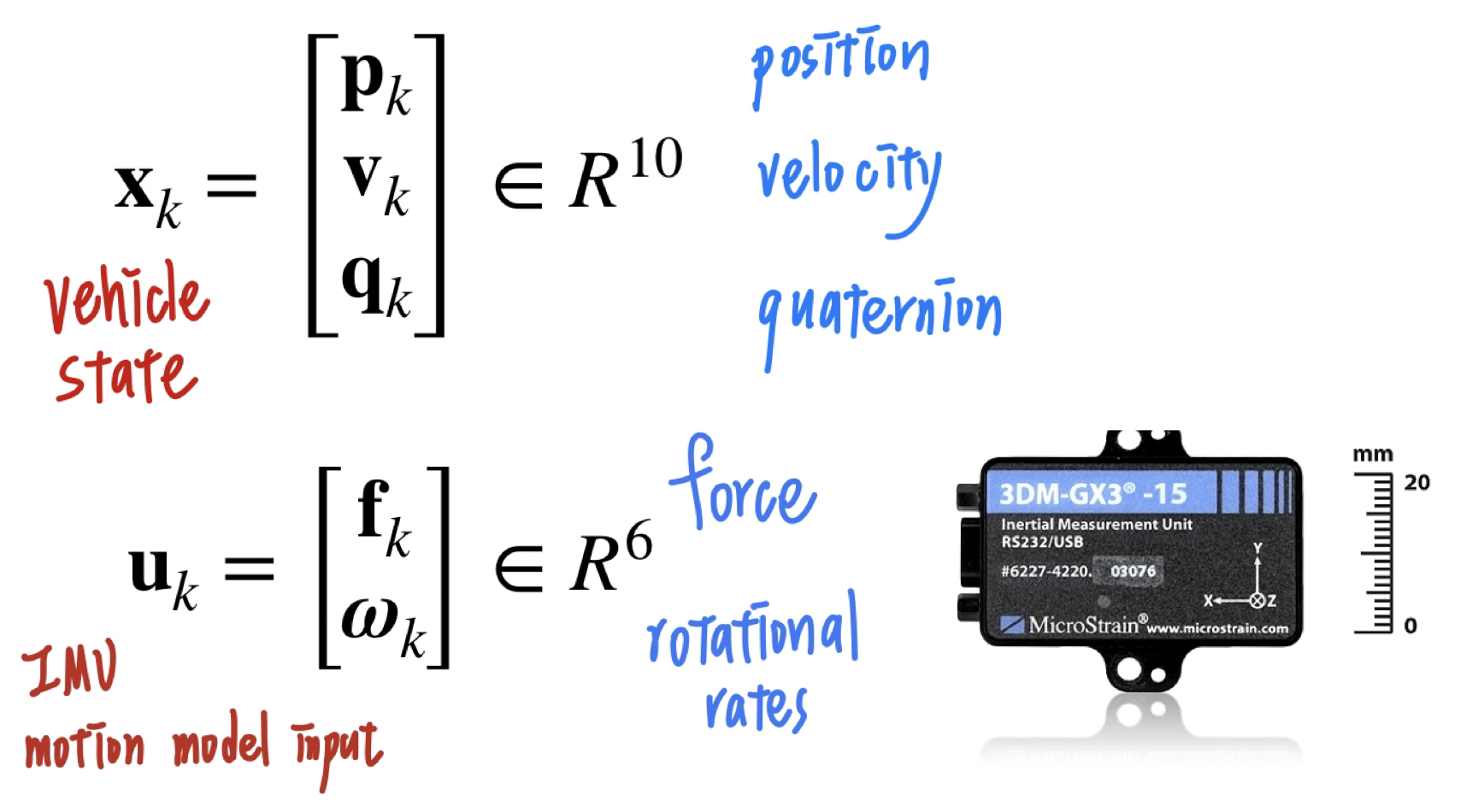
Use IMU to predict the state of the vehicle and correct the actual state with GNSS or LIDAR data.

What was achieved

  • Localized a vehicle with ES-EKF using prerecorded sensor data, including IMU, GPS, and LIDAR position updates
  • Examined the effects of sensor miscalibration on vehicle pose estimates, and adjusted the filter to compensate for errors
  • Investigated the effects of sensor dropout on the vehicle position estimate and the uncertainty in the position estimate

:computer: Github repo

Measurement update with Kalman filter

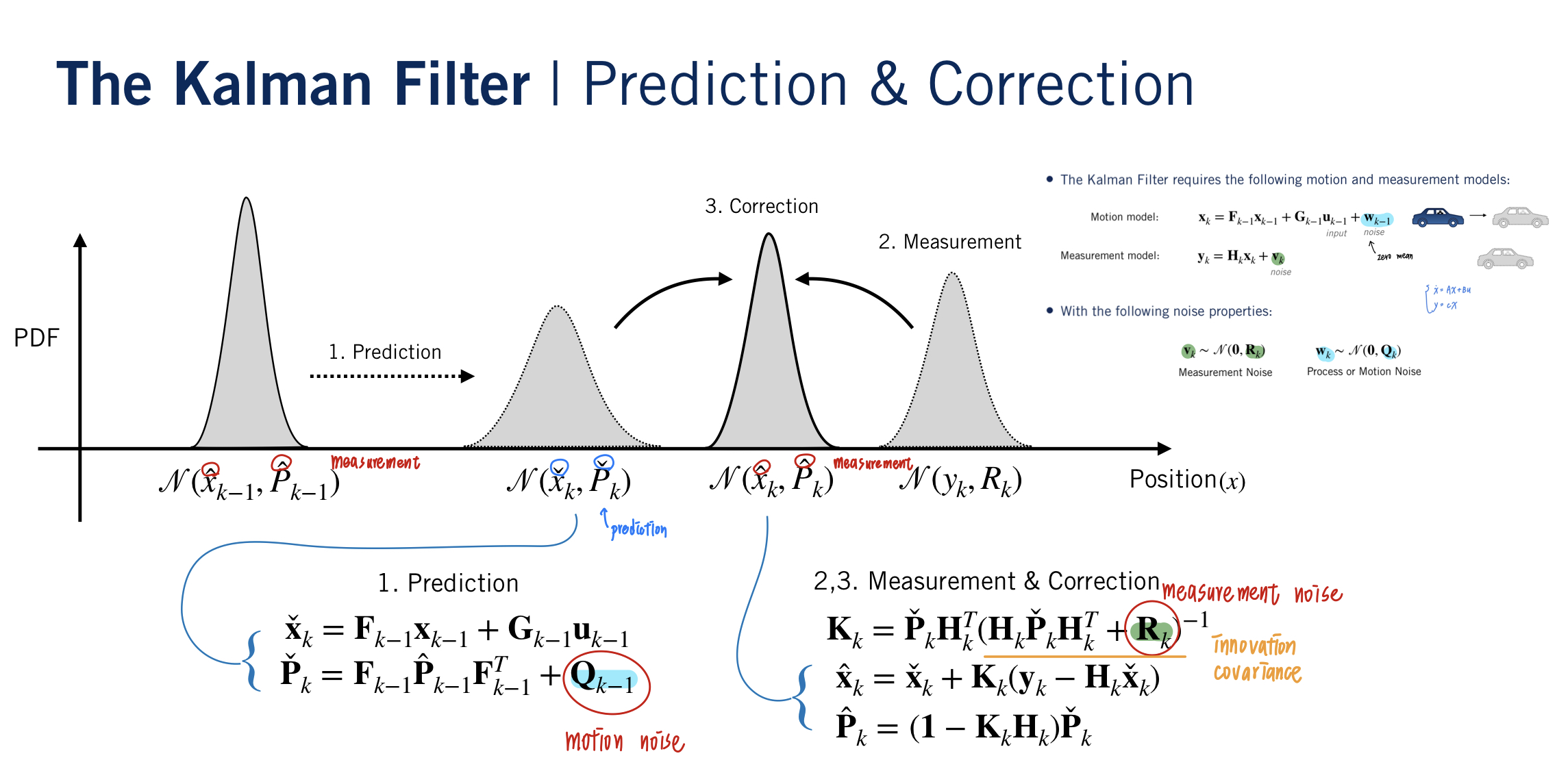
kalman filter

def measurement_update(sensor_v ar, p_cov_check, y_k, p_check, v_check, q_check):
    '''
    We update the measurement with both the GNSS and the LIDAR data.
    inputs
        - p_cov_check                 -> predicted covariance
        - y_k                         -> measurement
        - p_check, v_check, q_check   -> innovation
    '''
    
    # 3.1 Compute Kalman Gain
    R  = np.identity(3) * sensor_var   # change the sensor variance to covariance
    innovation_cov = h_jac.dot(p_cov_check).dot(h_jac.T) + R
    K = p_cov_check.dot(h_jac.T).dot(np.linalg.inv(innovation_cov))
    
    # 3.2 Compute error state
    sigma_x_hat = K.dot(y_k - p_check)
    
    # 3.3 Correct predicted state
    sigma_p = sigma_x_hat[:3]    # change in position
    sigma_v = sigma_x_hat[3:6]   # change in velocity
    sigma_phi = sigma_x_hat[6:]  # change in orientation
    
    # corrected
    p_hat = p_check + sigma_p    
    v_hat = v_check + sigma_v
    q_hat = Quaternion(euler=sigma_phi).quat_mult_right(q_check)
    
    # 3.4 Compute corrected covariance
    p_cov_hat = (np.identity(9) - K.dot(h_jac)).dot(p_cov_check)
    return p_hat, v_hat, q_hat, p_cov_hat

Main filter loop

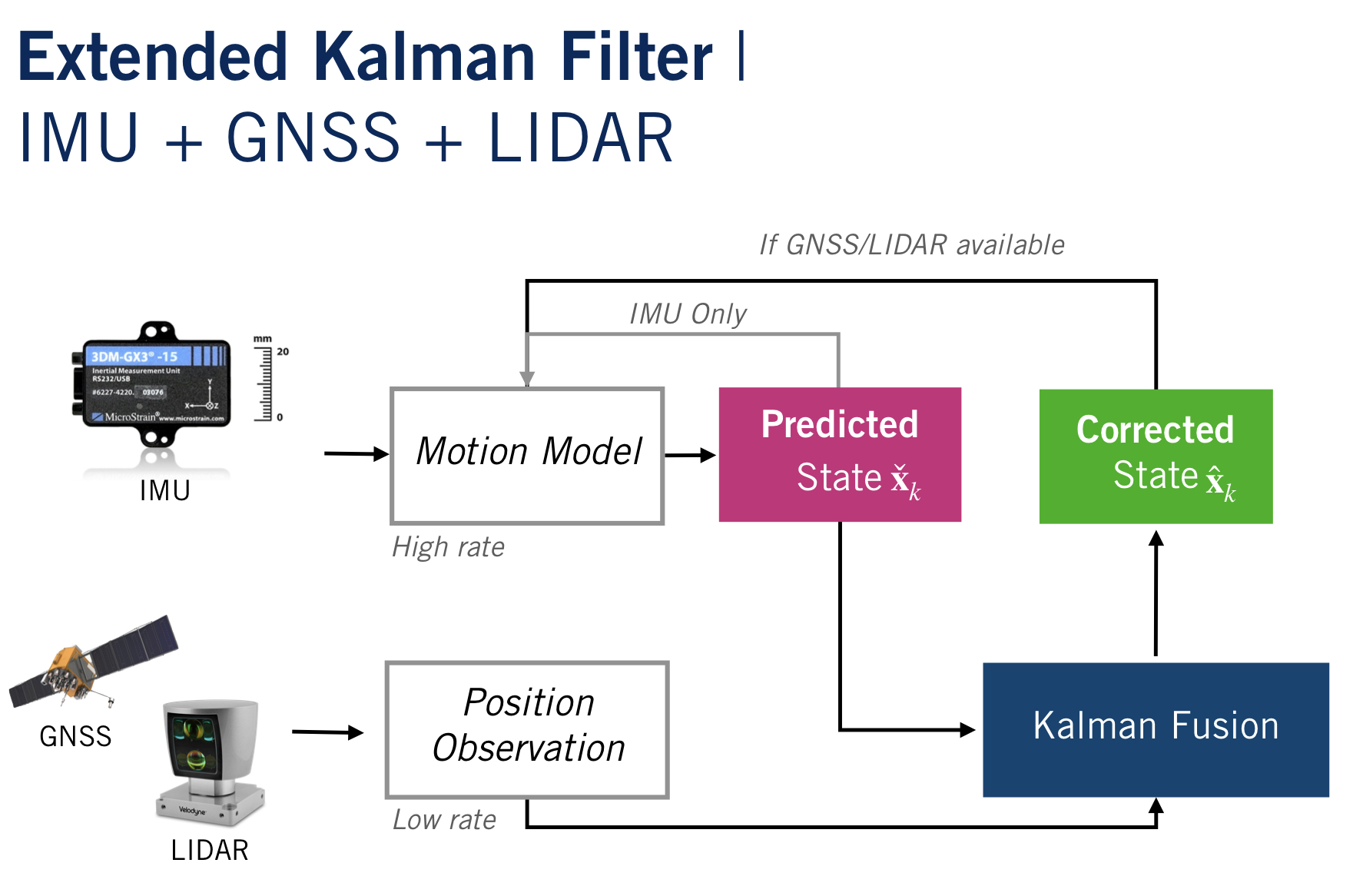
update flow

vehicle state and IMU model input Main loop
estimation trajectory main loop 
f = open("demofile2.txt", "a")

for k in range(1, imu_f.data.shape[0]):  # start at 1 b/c we have initial prediction from gt
    delta_t = imu_f.t[k] - imu_f.t[k - 1]

    # 1. Update state with IMU inputs
    C_ns = Quaternion(*q_est[k-1]).to_mat()    # C_ns (rotation matrix)
    C_ns_F_former = C_ns.dot(imu_f.data[k-1])  # C_ns * F_former

    # 1.1 Linearize the motion model and compute Jacobians
    # Position 
    p_est[k] = p_est[k-1] + delta_t*v_est[k-1] + (delta_t**2 / 2)*(C_ns_F_former + g)
    # Velocity
    v_est[k] = v_est[k-1] + delta_t*(C_ns_F_former + g)
    # Orientation
    q_est[k] = Quaternion(axis_angle=imu_w.data[k-1] * delta_t).quat_mult_right(q_est[k-1])
    
    # 2. Propagate uncertainty
    F = np.identity(9)
    Q = np.identity(6)
    F[0:3, 3:6] = np.identity(3) * delta_t
    F[3:6, 6:9] = -(C_ns.dot(skew_symmetric(imu_f.data[k-1].reshape((3,1)))))
    Q[:, :3] *= delta_t**2 * var_imu_f
    Q[:, -3:] *= delta_t**2 * var_imu_w
    p_cov[k] = F.dot(p_cov[k-1]).dot(F.T) + l_jac.dot(Q).dot(l_jac.T)
  
    # 3. Check availability of GNSS and LIDAR measurements
    if (lidar_i < lidar.t.shape[0]) and (lidar.t[lidar_i] == imu_f.t[k-1]):
        p_est[k], v_est[k], q_est[k], p_cov[k] = measurement_update(var_lidar, p_cov[k], lidar.data[lidar_i].T, p_est[k], v_est[k], q_est[k])
        lidar_i += 1
    if (gnss_i < gnss.t.shape[0]) and (gnss.t[gnss_i] == imu_f.t[k-1]):
        p_est[k], v_est[k], q_est[k], p_cov[k] = measurement_update(var_gnss, p_cov[k], gnss.data[gnss_i].T, p_est[k], v_est[k], q_est[k])
        gnss_i += 1
    

f.close()
    # Update states (save)
    #already updated

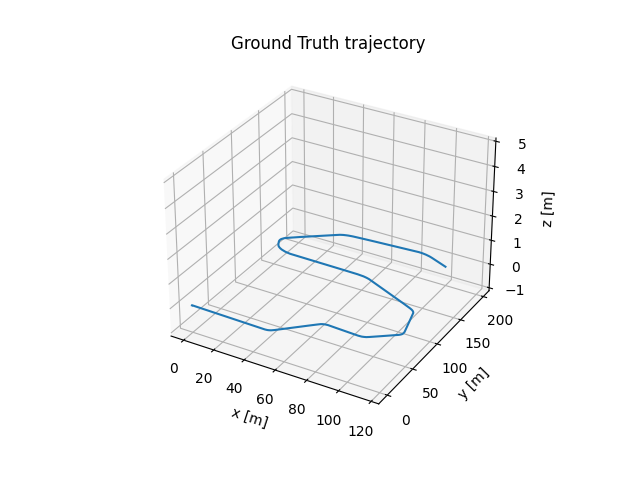
Final results

Ground Truth Estimation
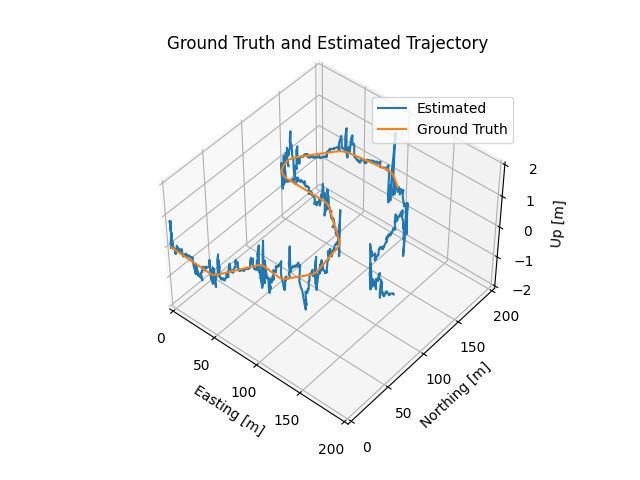ground truth trajectory estimation trajectory